MIT 算法导论(2) - 渐进符号,递归式解法,学习记录
这节课主要是讲解各种渐进符号的含义,以及求解递归式的方法。讲课老师是Erik Demaine,MIT历史上最年轻的教授。
当分析算法时,其实有五种渐进符号,我们平时用的大O表示法,其实只是其中一种,也称作最糟运行时间(<=);当我们说一个算法的时间复杂度等于O(n)的时候,其实不是真正的等于,是小于或者等于,属于是的含义。
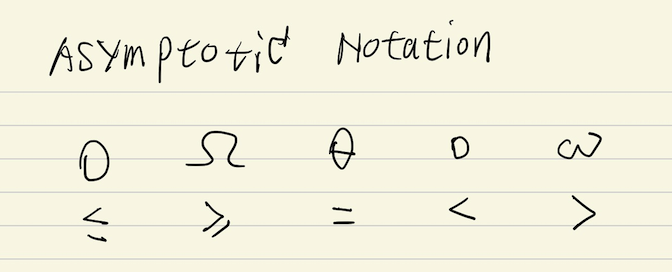
接下来主要是讲解,求解递归式的三种方法:
- 代换法
- 递归树法
- 主方法(Master Method)
听下来感觉这三个方法都不够完美,代换法,主要靠猜 :);递归树法,有点不严谨;主方法,比较好,但是限制条件很多,只能应用于特定的递归式上面。
由于后面课程需要用到主方法,因此主方法需要重点掌握。
总的说来这节课,数学证明有点多,比较偏重于理论,如果觉得比较枯燥,可以匆匆跳过,直接看第三课,如果后面有用到该课的知识点,再回过头来翻看也不迟。